分極率

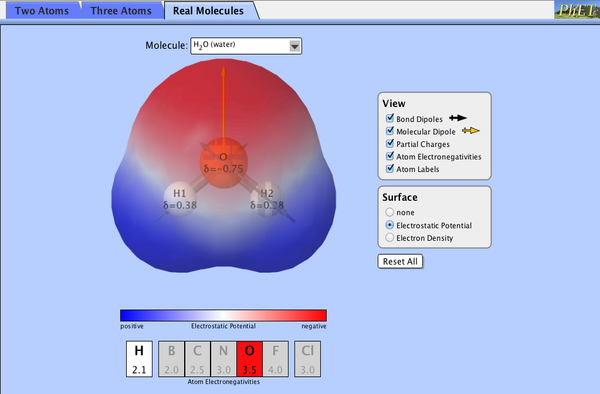
分極率(ぶんきょくりつ、polarizability)とは、原子や分子の電子雲などがもつ電荷分布の相対的な偏りを表す物理量である。電荷分布は近くに存在するイオンや双極子の存在などによって引き起こされる外部電場によって歪められる。この歪められた電荷分布の通常の状態からの偏差が分極率である。

古典論

等方的な系において、分極率${\displaystyle \alpha }$は電場${\displaystyle {\boldsymbol {E}}}$とこの電場により誘起された原子、分子の誘起双極子モーメント${\displaystyle {\boldsymbol {p}}}$の比として定義される。

${\displaystyle {\boldsymbol {p}}=\alpha {\boldsymbol {E}}}$

分極率は、国際単位系ではC·m²·V^-1 = A²·s⁴·kg^-1の次元をもつが、しばしばcm³またはų = 10^-24 cm³の次元をもつ分極率体積によってあらわされる。

${\displaystyle \alpha \,({\textrm {cm}}^{3})={\frac {10^{6}}{4\pi \epsilon _{0}}}\alpha \,({\textrm {C}}\cdot {\textrm {m}}^{2}\cdot {\textrm {V}}^{-1})}$

ここで${\displaystyle \epsilon _{0}}$は真空の誘電率である。

個々の粒子(分子)の分極率はミクロな量であり、マクロな量である媒質の平均電気感受率との間にはクラウジウス・モソッティの関係で結びついている。

上記で定義された分極率${\displaystyle \alpha }$はスカラー量であり、加えられた電場と誘起された分極は平行であるが、異方的な系においてはそうならないことがある。 その場合分極率${\displaystyle {\boldsymbol {\alpha }}}$は2階のテンソルとして定義される（等方的な系のものは単位行列で ${\displaystyle {\boldsymbol {\alpha }}=\alpha {\boldsymbol {1}}}$と表現できる）。

量子論

量子論的に導かれる分極率テンソルのρσ成分は次のように表される。

${\displaystyle \alpha _{\rho \sigma }=\sum _{e\neq g}{\bigg \{}{\frac {[g|D_{\sigma }|e][e|D_{\rho }|g]}{h(\nu _{e}-\nu _{g}-\nu _{I})}} {\frac {[g|D_{\sigma }|e][e|D_{\rho }|g]}{\nu _{e}-\nu _{g} \nu _{I}}}{\bigg \}}}$

ここで${\displaystyle |\quad ]}$は、状態ケットを断熱近似によって電子部分と振動部分に分解したときの、電子部分のケットである。

クラマース・ハイゼンベルグの分散式は、Placzekの分極率近似をすることで、分子の分極率テンソルで近似的に表される。

中性原子の分極率の一覧

以下の値の多くは計算により求められたものである。

参考文献

• 田隅三生, 浜口宏夫「ラマン分光の基礎」（｢赤外・ラマン・振動[I]｣(化学の領域 増刊 139号), 坪井正道・田中誠之・田隅三生編, 南江堂, pp. 19-30 (1983年)）
• 浜口宏夫、平川暁子編：ラマン分光法、学会出版センター、1988年、ISBN:4762215686.
• G. Maroulis編：Atoms, Molecules And Clusters in Electric Fields: Theoretical Approaches to the Calculation of Electric Polarizability（Ch. 1）、World Scientific Publishing Company、2006年、ISBN:1860946763

関連項目

• クラマース・ハイゼンベルグの分散式